Probabilistic State Estimation with an Unscented Kalman Filter

Project Overview

This project implements an Unscented Kalman Filter (UKF) to estimate the planar pose of a differential-drive robot. The state is defined as \( \mathbf{x} = [x, y, \theta]^T \) and is estimated from noisy velocity commands and beacon-based measurements.

Performance is compared directly against dead reckoning to demonstrate the benefit of probabilistic state estimation under uncertainty.

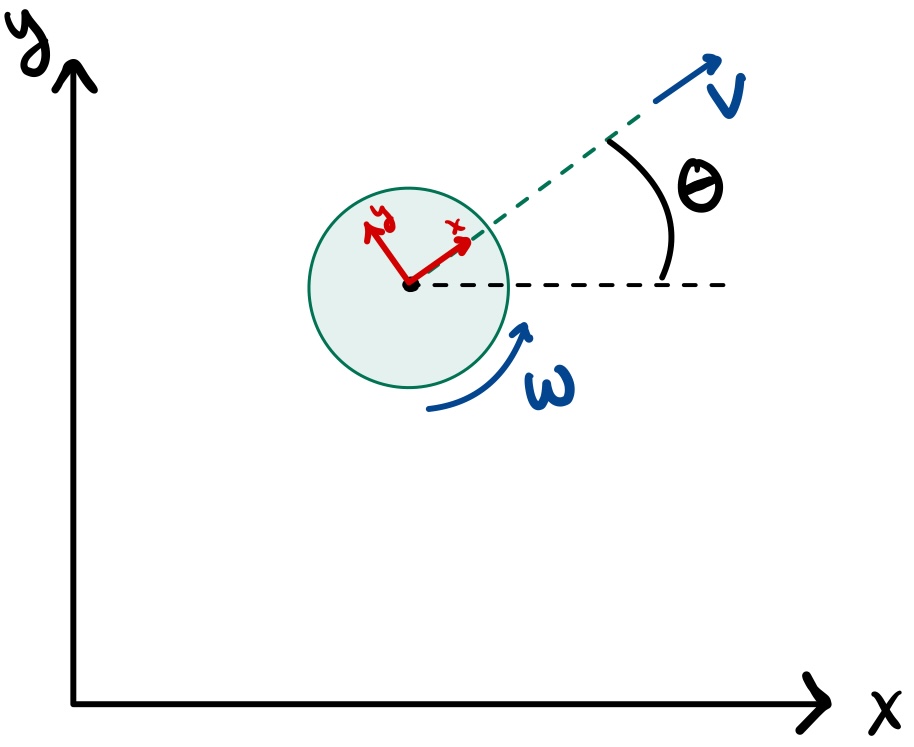
Motion Model

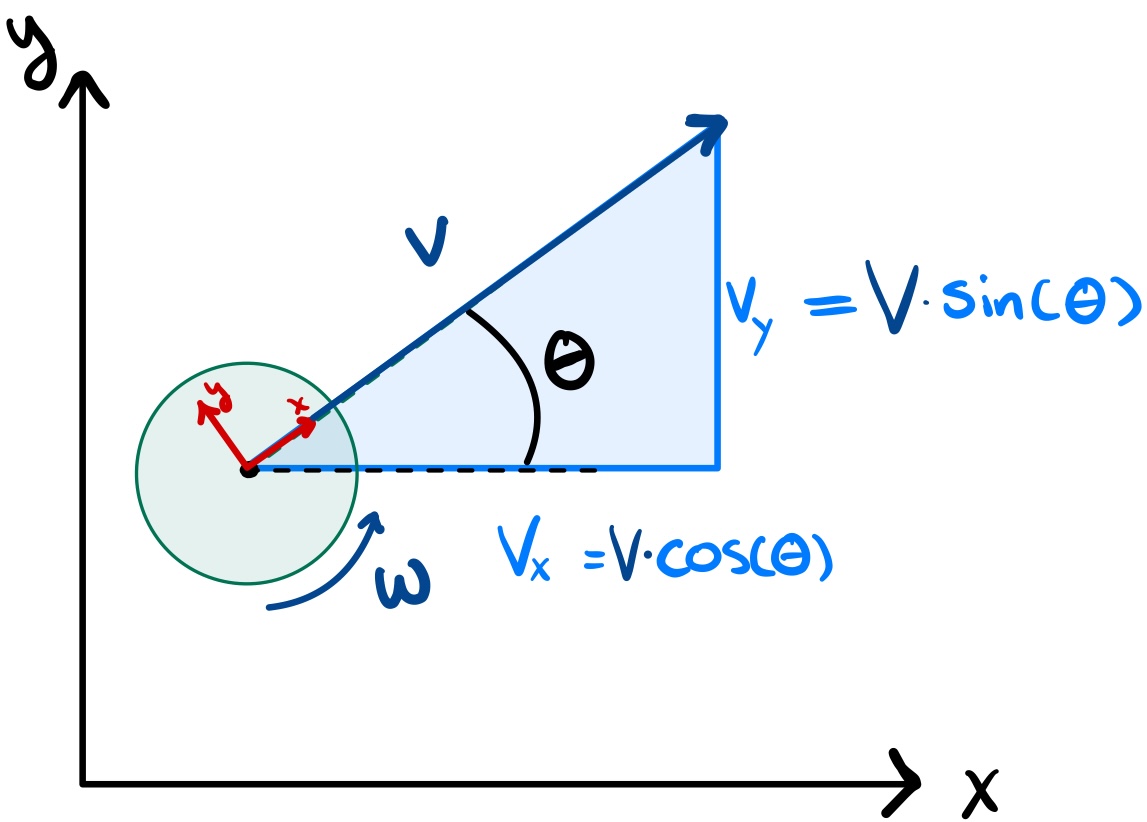
The robot motion model assumes a differential-drive platform driven by linear and angular velocity commands \( \mathbf{u} = [v, \omega] \). Over a discrete timestep \( \Delta t \), the motion model is:

\[ \begin{aligned} x_{k+1} &= x_k + v \cos(\theta_k)\Delta t \\ y_{k+1} &= y_k + v \sin(\theta_k)\Delta t \\ \theta_{k+1} &= \theta_k + \omega \Delta t \end{aligned} \]

Gaussian process noise is added to account for actuator uncertainty, wheel slip, and unmodeled dynamics. This model is used both for dead reckoning and the UKF prediction step.

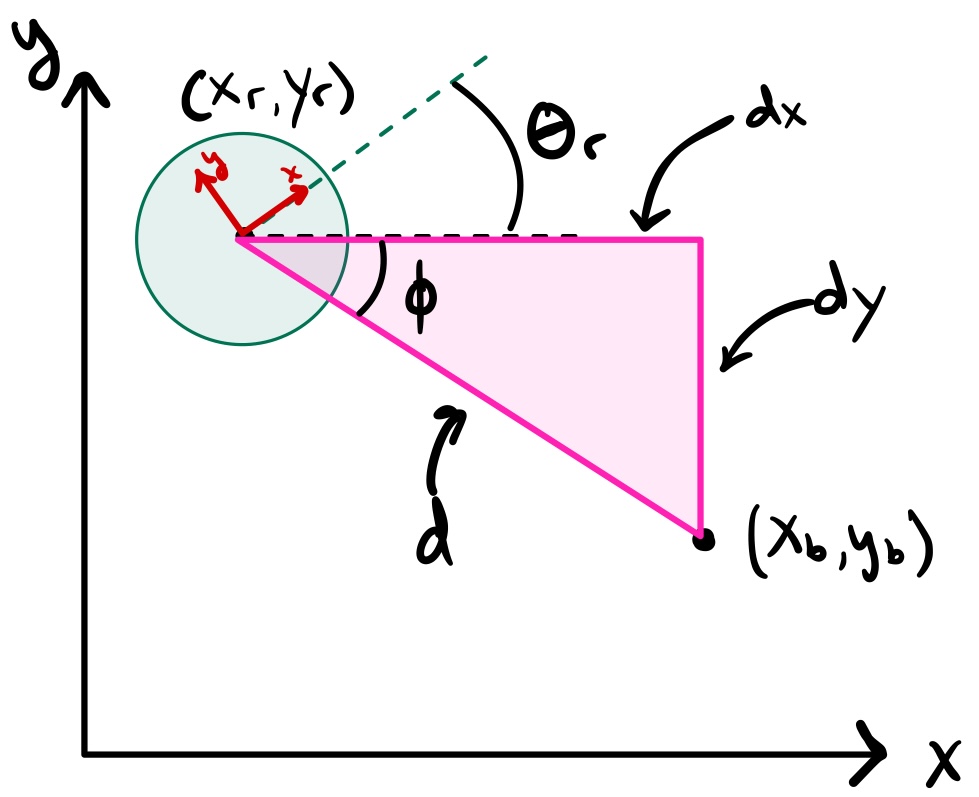
Measurement Model

Measurements consist of range and bearing observations to known beacons at positions \( (x_b, y_b) \). The nonlinear measurement model is:

\[ \begin{aligned} r &= \sqrt{(x - x_b)^2 + (y - y_b)^2} \\ \phi &= \mathrm{atan2}(y_b - y, x_b - x) - \theta \end{aligned} \]

Measurement noise is modeled as zero-mean Gaussian noise applied to both range and bearing. These nonlinear equations motivate the use of a UKF rather than a linearized EKF.

Unscented Kalman Filter

The Unscented Kalman Filter propagates uncertainty through nonlinear dynamics using deterministically chosen sigma points that capture the mean and covariance of the state distribution.

Unlike the Extended Kalman Filter, the UKF does not require Jacobians. Instead, sigma points are passed through the nonlinear motion and measurement models and recombined to update the state estimate.

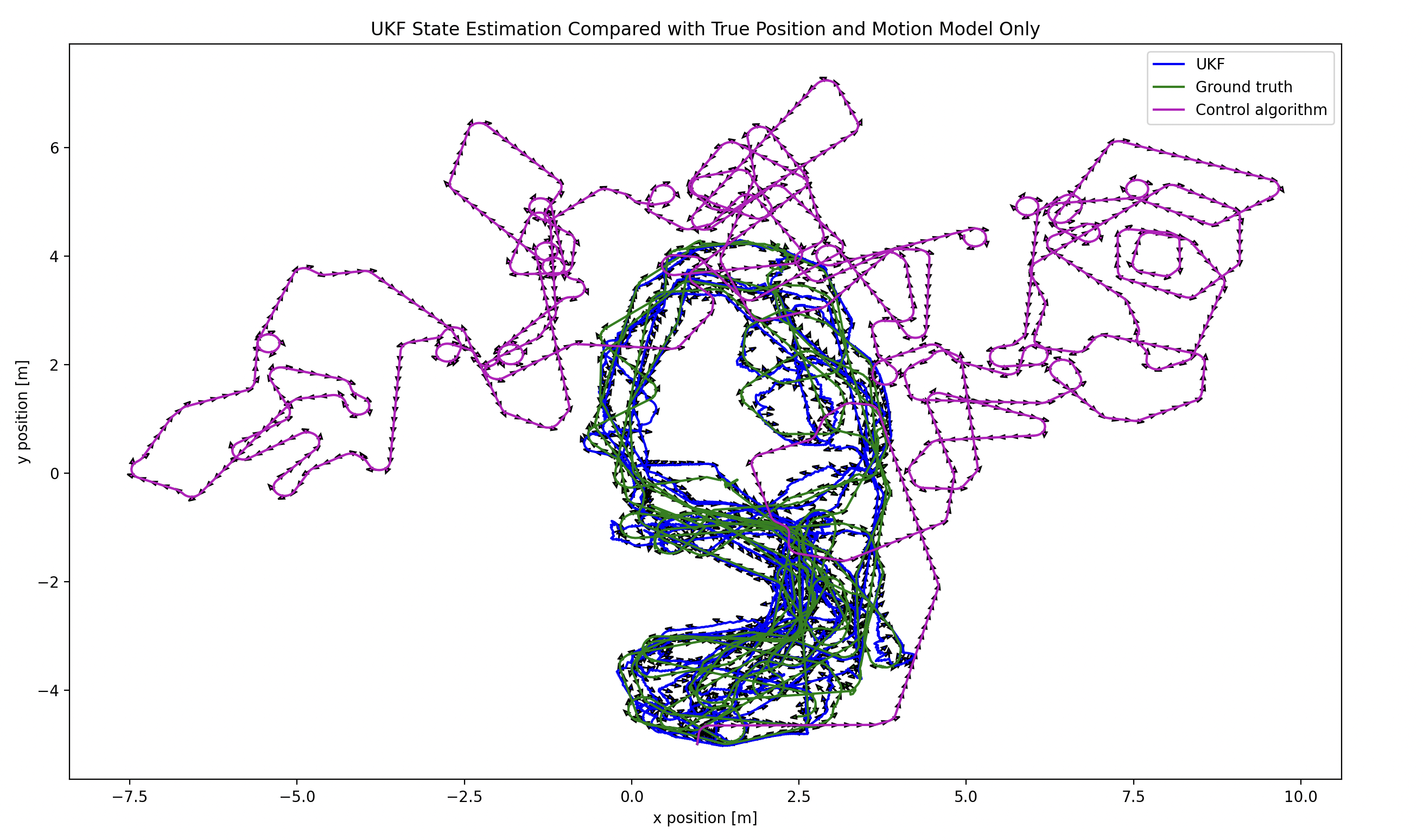
Performance Comparison

Dead reckoning accumulates error over time due to uncorrected process noise, resulting in significant drift in both position and orientation.

The UKF continuously corrects state estimates using beacon measurements, keeping estimation error bounded throughout the trajectory.

Reflections

This project demonstrated the limitations of purely kinematic estimation and the effectiveness of probabilistic filtering. Implementing the UKF from scratch provided valuable insight into uncertainty propagation and sensor fusion for mobile robots.