Physics Simulation – Lagrangian Impacts (Jack-in-Box)

Project Overview

For this MECH_ENG 314 capstone, I modeled the dynamics of a jack-in-a-box in 2D, applying advanced Lagrangian mechanics and computational methods to capture both free motion and impacts. This project combines analytical physics, rigorous coding, and visualization—a full pipeline from equations to simulation.

System Modeling and Setup

• Both box and jack are described by positions and angles: \((x, y, \theta)\) for each.
• All reference frames and transformations are defined analytically. Symbolic expressions (via SymPy) allow automatic differentiation for velocities and energies.
• The homogenous transformation matrices link every object’s frame to the world frame {w}, allowing us to check for impact conditions and later display the simulated system
  
  
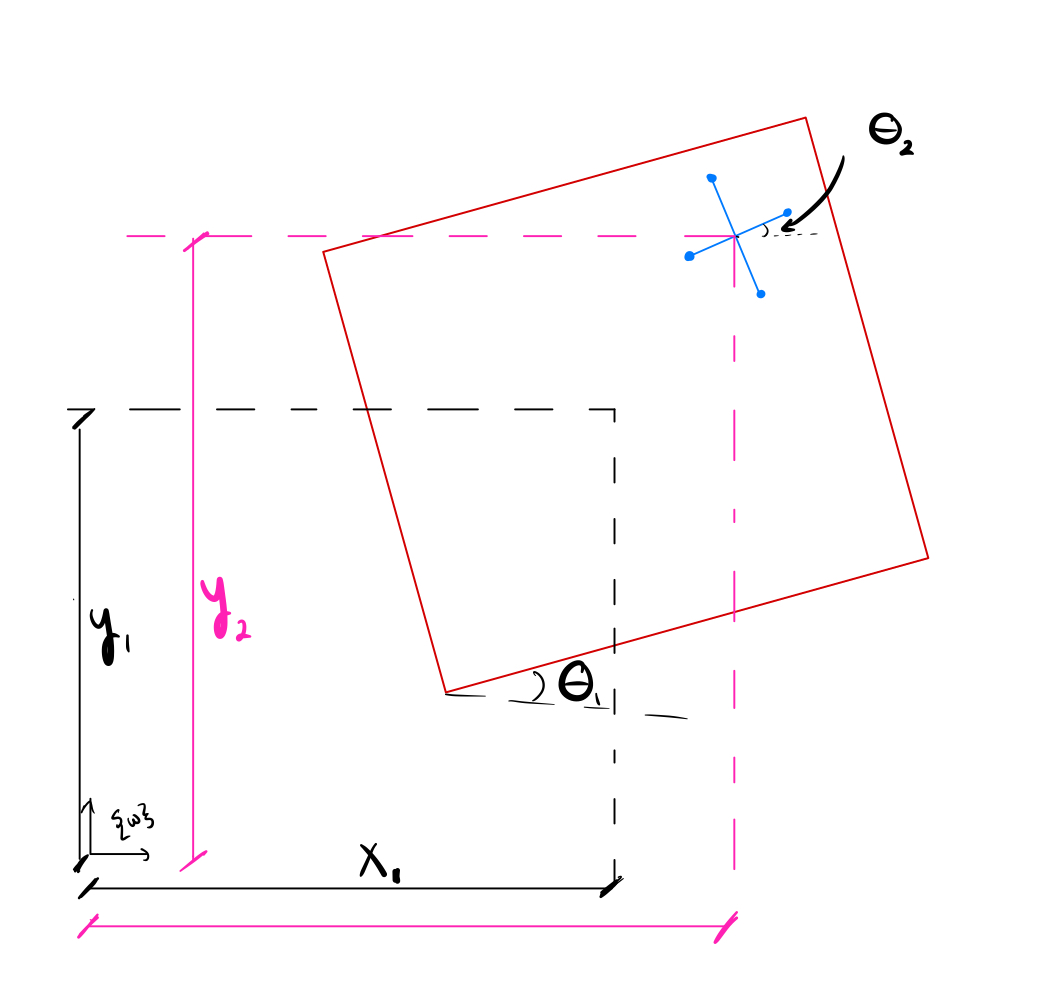
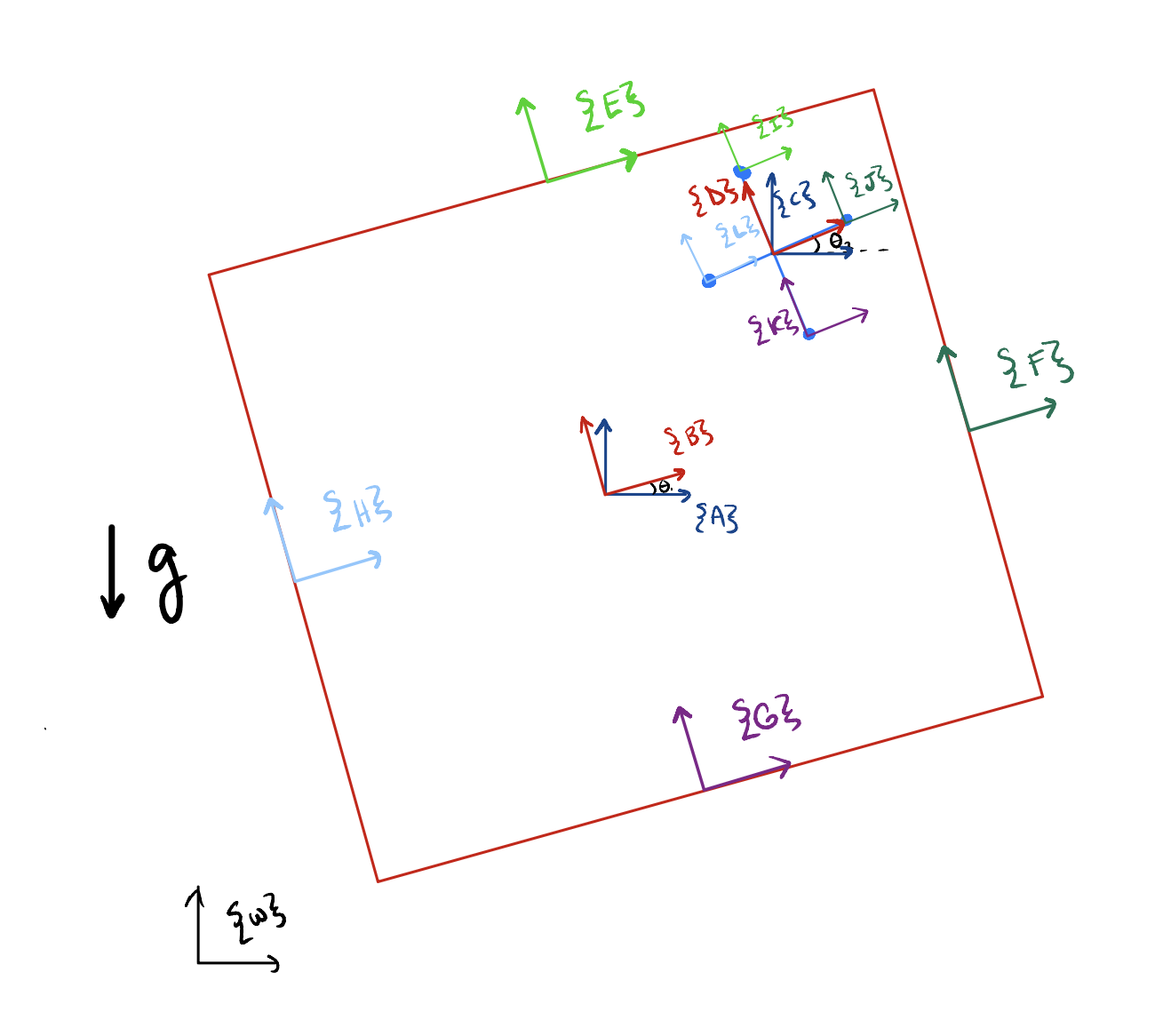  Configuration and reference frames for the jack and box

Euler-Lagrange Equations & Solution

• By the Action Principle - we know a particle will take the path of least local action. Therefore, if we integrate its action (the Legrangian) over a path, we know the particle will follow the configuration of least energy/action.
• So, by solving \(\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_i}\right) - \frac{\partial L}{\partial q_i} = F_{external}\) we can simulate the systems behavior

External Forces

• Gravity compensation: Upward force equal to four times box-side weight, keeps box in frame.
• Box torque: Sustains box spinning and creates repeated impacts.
• Shaking force: Time-dependent horizontal force, implemented using SymPy’s Heaviside for piecewise control.

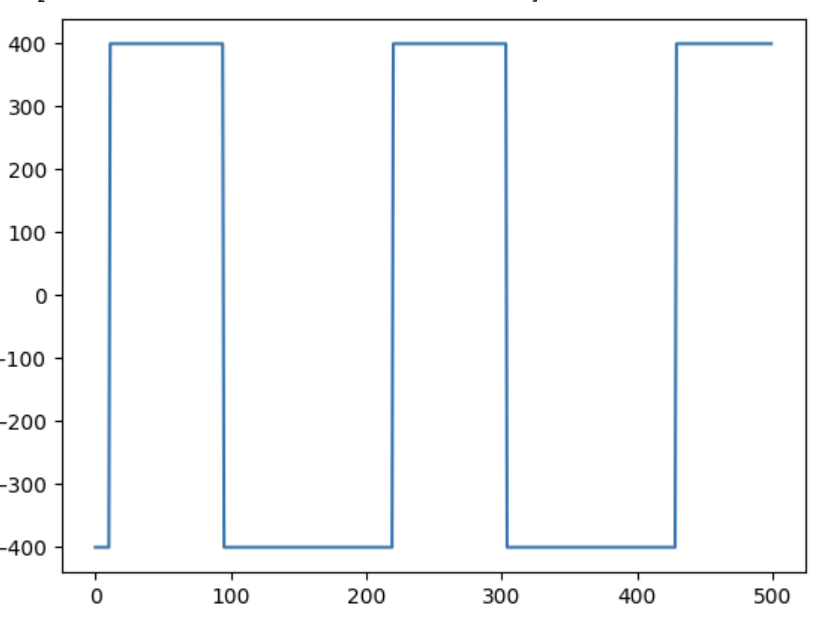
Impact Events & Update Laws

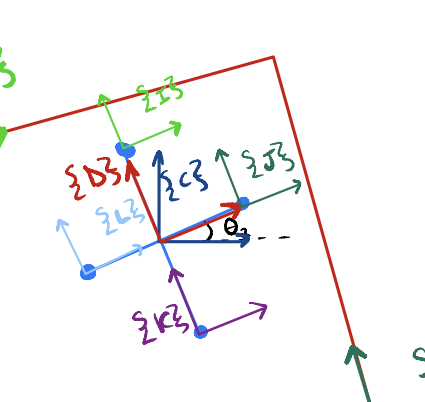
• Impact Detection: 16 impact “phi” conditions, one for each jack point contacting each box side. Evaluated by transforming jack-tip location into each box frame and checking for intersection (\(x\) or \(y\) coordinate crossing zero).
• Impact Response: On detection, update laws conserve momentum as per Hamiltonian and Lagrangian matching. The update equations are solved symbolically and applied to the post-impact state, resulting in an elastic collision.
• Example: For the configuration below, we need to check if frame {J} has crossed the y-axis of frame {F} below which is in line with the right wall of the box.

Simulation & Results

• Numerical integration is handled by a Runge-Kutta 4 (RK4) scheme.
• Each RK4 step includes impact checks; if triggered, velocities and positions are updated immediately according to impact laws, then simulation resumes.

Reflections

This project challenged me to combine symbolic math, mechanical insight, and robust numerical methods. Coding these mechanics from the ground up, I deepened my understanding of Lagrangian analysis and impact mechanics, and demonstrated a full workflow from equations to animation.