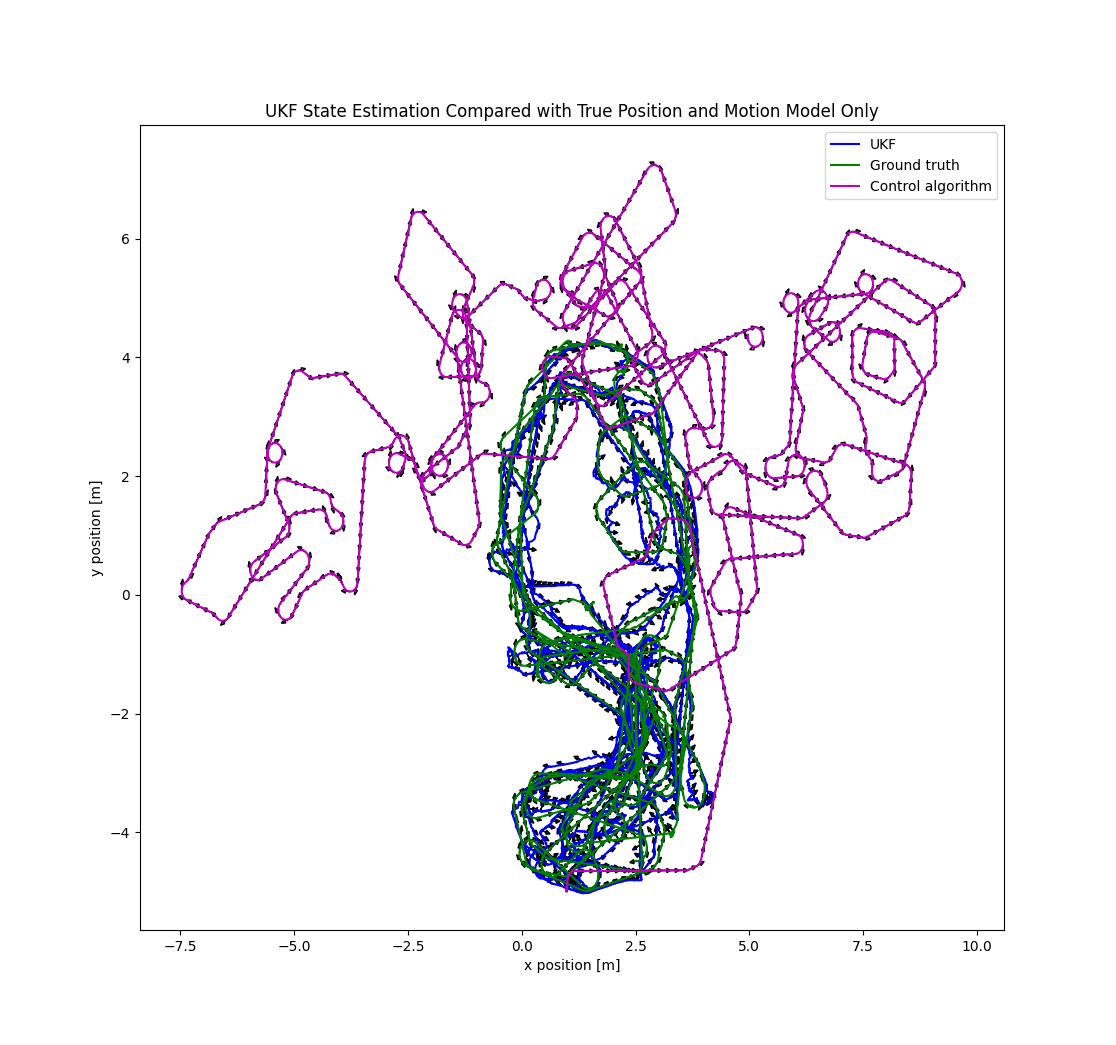
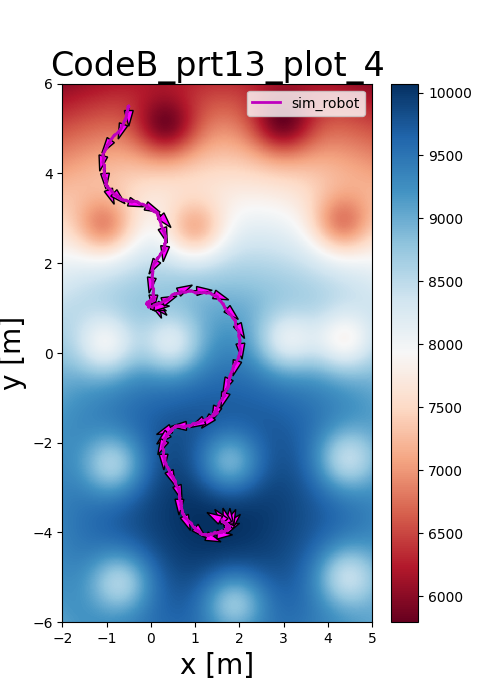
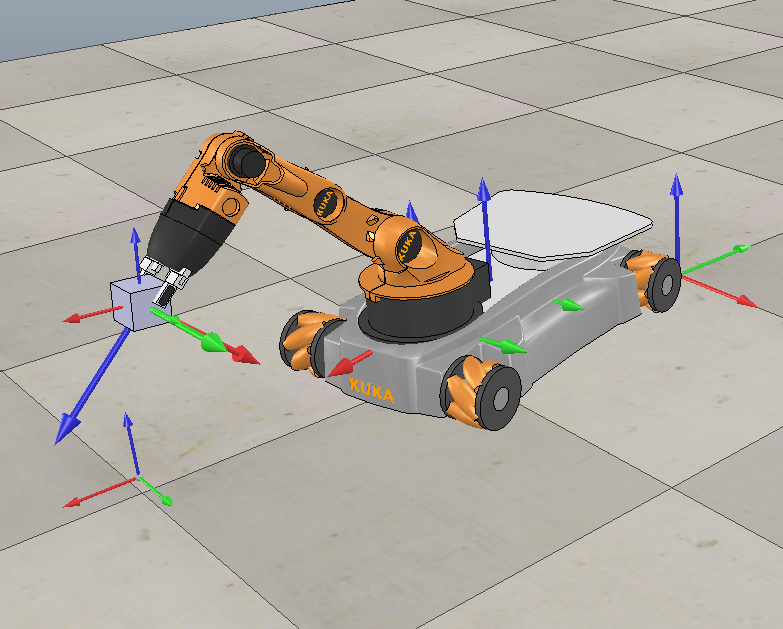
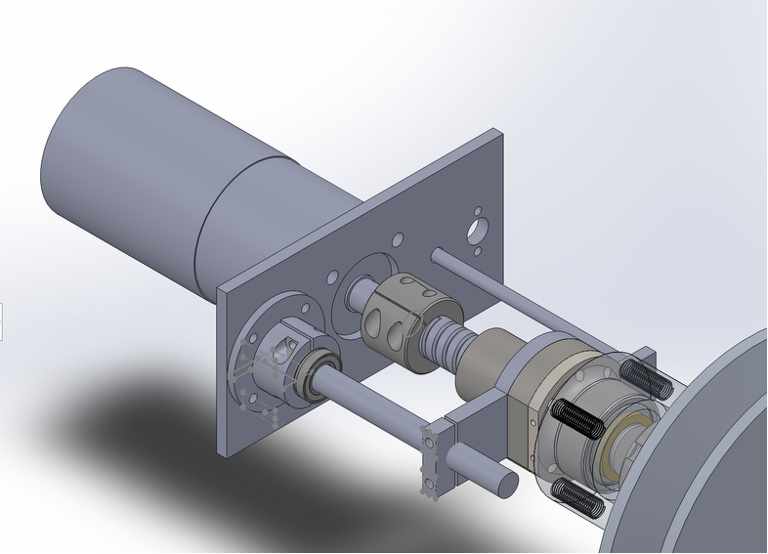
Welcome!
Hi, my name is Michael. Thanks for checking out my portfolio.
I am graduating in the Spring of 2026 with my Bachelors and Masters in Mechanical Engineering with specialization in robotics.
I have focused my masters research on the design of a mechatronic prosthetic arm.
If you'd like to hear more, please help yourself to these links below.
Links:
Contact Me
Feel free to reach out to me through any of the methods below:
- Email: michael.jenz77@gmail.com
- Phone: +1 (630) 470-0104
- LinkedIn: linkedin.com/in/michael-jenz